What's Bigger 1 4 Or 1 8

Comparing fractions and understanding their relative sizes is an essential skill in mathematics. In this article, we delve into the concept of comparing fractions and specifically tackle the question: Which is bigger, 1/4 or 1/8? We will explore the methods to compare these fractions, provide real-world examples, and offer insights into the practical applications of this knowledge.

Understanding Fraction Comparison

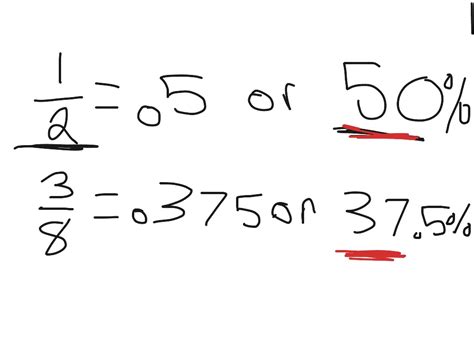
Comparing fractions is a fundamental mathematical operation that allows us to determine which fraction is larger or smaller than another. It involves recognizing the relationship between the numerator (the top number) and the denominator (the bottom number) of each fraction. When comparing ¹⁄₄ and ¹⁄₈, we need to identify which fraction represents a larger portion or quantity.

Methods for Comparing Fractions

There are several methods to compare fractions, and understanding these methods is crucial for accurate comparisons. Let’s explore some of the most common approaches:

• Common Denominator Method: This method involves finding a common denominator for the two fractions. By converting them to equivalent fractions with the same denominator, we can easily compare their numerators. For example, we can express ¹⁄₄ as ²⁄₈ by multiplying both the numerator and denominator by 2, and ¹⁄₈ as ¹⁄₈ (no change needed). Now, it’s clear that ²⁄₈ is larger than ¹⁄₈.
• Comparing by Parts: Another approach is to compare the numerators and denominators separately. If the numerators are the same, the fraction with the smaller denominator is larger. Conversely, if the denominators are the same, the fraction with the larger numerator is greater. In our case, ¹⁄₄ has a larger numerator (1) than ¹⁄₈, indicating that ¹⁄₄ is the larger fraction.
• Visual Representation: Using visual aids such as fraction bars or circle diagrams can help illustrate the comparison. By dividing a whole into fourths and eighths, we can physically see that ¹⁄₄ represents a larger portion than ¹⁄₈.

Real-World Applications

The ability to compare fractions is not just a theoretical concept; it has numerous practical applications in everyday life. Here are a few examples:

• Cooking and Baking: When following a recipe, you might need to adjust ingredient quantities. Understanding fraction comparison helps you make precise measurements, ensuring your dish turns out perfectly.
• Finance and Budgeting: Fractions are often used to represent percentages in financial contexts. Being able to compare fractions allows you to analyze investment returns, calculate discounts, or plan budgets more effectively.
• Sports and Statistics: In sports, fractions are used to express win percentages, success rates, or scoring averages. Comparing these fractions can provide valuable insights into team or player performance.

Comparison Analysis: ¹⁄₄ vs. ¹⁄₈

Now, let’s apply our understanding of fraction comparison to the specific fractions ¹⁄₄ and ¹⁄₈.

Using the Common Denominator Method

As mentioned earlier, finding a common denominator is a reliable way to compare fractions. In this case, we can use the least common denominator (LCD) of 8. By converting ¹⁄₄ to an equivalent fraction with a denominator of 8, we get ²⁄₈. So, our comparison becomes ²⁄₈ vs. ¹⁄₈. Clearly, ²⁄₈ is larger than ¹⁄₈, indicating that ¹⁄₄ is the bigger fraction.

Visual Representation

Let’s visualize the comparison using a simple bar model. Imagine a whole divided into fourths and eighths. When we compare the lengths of ¹⁄₄ and ¹⁄₈, it becomes evident that ¹⁄₄ represents a larger portion of the whole, making it the bigger fraction.

Practical Example: Baking a Cake

Consider a scenario where you’re baking a cake, and the recipe calls for ¹⁄₄ cup of sugar. However, you only have a measuring cup marked with eighths. You need to determine how many ¹⁄₈ cup measurements you’ll need to make up the required ¹⁄₄ cup of sugar. By comparing the fractions, you realize that ¹⁄₄ is equivalent to ²⁄₈, so you’ll need 2 ¹⁄₈ cup measurements to achieve the desired quantity.