How to Find Your Stable Match
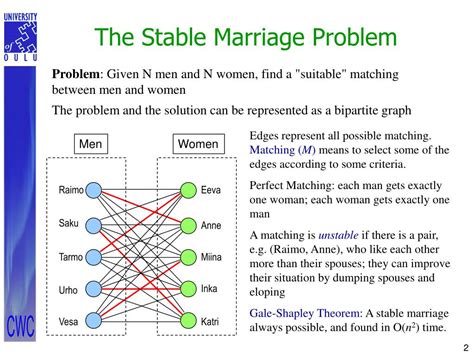
In the complex world of algorithms and optimization, the Stable Marriage Problem, or Stable Matching Problem, stands as a fascinating and practical mathematical conundrum. This problem, with its roots in game theory, has broad applications, from student-school assignments to organ donation matching, and even in the realm of online dating. In this article, we delve into the intricacies of the Stable Matching Problem, exploring its history, underlying mathematics, and its relevance in our daily lives.
Understanding the Stable Matching Problem
At its core, the Stable Matching Problem is a combinatorial algorithm designed to find a stable matching between two sets of elements, often represented as individuals or entities with preferences. The objective is to create a matching, or pairing, that satisfies certain criteria, ensuring that no pair of elements would rather be matched with each other than remain with their current partners.
The concept was first introduced by Lloyd Shapley and David Gale in the 1960s to solve the problem of matching students to universities. Since then, it has evolved into a powerful tool used in various fields, including economics, computer science, and social sciences.
Key Definitions
- Matching: A pairing of elements from two sets. In the context of the Stable Marriage Problem, it represents the assignment of individuals to their preferred partners.
- Stable Matching: A matching where there are no unsatisfied or dissatisfied pairs. This means that there is no pair of individuals who are not currently matched together but prefer each other over their current partners.
- Preferences: The order of preference that each individual has for the other set of elements. These preferences are often represented as a ranking or list.
To better understand the Stable Matching Problem, let's consider a simplified example. Imagine a group of five men and five women, each with their own preferences for potential partners. The goal is to find a stable matching, where no two individuals would rather be with each other than with their assigned partners.
| Men | Women | Preferences |
|---|---|---|
| Adam | Emma | 1. Emma 2. Grace 3. Lily 4. Olivia 5. Sarah |
| Ben | Grace | 1. Grace 2. Emma 3. Sarah 4. Lily 5. Olivia |
| Chris | Lily | 1. Lily 2. Sarah 3. Emma 4. Olivia 5. Grace |
| David | Olivia | 1. Olivia 2. Sarah 3. Emma 4. Grace 5. Lily |
| Ethan | Sarah | 1. Sarah 2. Emma 3. Grace 4. Olivia 5. Lily |

The Gale-Shapley Algorithm: A Stable Solution

The Gale-Shapley algorithm, also known as the Deferred Acceptance algorithm, is a well-known solution to the Stable Matching Problem. It is a non-constructive algorithm, meaning it does not directly build the solution, but rather proves its existence and provides a method to find it.
How it Works
- Each man proposes to the woman he prefers most.
- If a woman receives multiple proposals, she keeps the proposal from the man she prefers most and rejects the others.
- Rejected men move down their preference list and propose to their next preferred woman.
- This process continues until all men are matched or there are no more proposals.
The resulting matching is always stable, ensuring that no two individuals prefer each other over their assigned partners. While the Gale-Shapley algorithm guarantees stability, it does not always produce a matching that is fair or optimal for all participants.
Example Application: College Admissions
In the context of college admissions, the Stable Matching Problem can be used to match students to their preferred colleges. Each student has a list of colleges they would like to attend, ranked in order of preference. Similarly, colleges have their own preferences for students, often based on academic performance and other criteria.
By applying the Gale-Shapley algorithm, a stable matching can be found, ensuring that no student and college would prefer to be matched with each other over their current assignments. This helps to reduce the chances of students being left unmatched or colleges being unable to fill their seats.
Real-World Applications and Challenges
The Stable Matching Problem and its algorithms have found numerous real-world applications, extending beyond college admissions. Some notable examples include:
- Kidney Exchange Programs: Stable matching algorithms are used to facilitate kidney exchanges, ensuring that donors and recipients are matched in a fair and stable manner.
- Job Assignment: Companies can use stable matching to assign employees to specific roles or projects, considering both employee preferences and company needs.
- Housing Allocation: Stable matching can be applied to allocate housing units to residents, considering their preferences and other factors such as family size and income.
However, despite its wide-ranging applications, the Stable Matching Problem is not without its challenges. One of the main criticisms is the lack of consideration for individual fairness. While the matching is stable, it may not be optimal for all participants, leading to potential dissatisfaction.
Additionally, the problem assumes that preferences are known and static, which may not always be the case in real-world scenarios. Individuals' preferences can change over time, and there may be uncertainty or hidden preferences that are not easily expressed.
Future Directions and Research
The Stable Matching Problem continues to be an active area of research, with ongoing efforts to improve its efficiency, fairness, and applicability to various domains. Researchers are exploring:
- Fairness Metrics: Developing new metrics to measure and improve the fairness of stable matchings, ensuring that all participants are treated equitably.
- Dynamic Preferences: Investigating methods to incorporate dynamic preferences, where individuals' rankings can change over time, into stable matching algorithms.
- Machine Learning Integration: Exploring the use of machine learning techniques to optimize stable matching, especially in scenarios with large datasets and complex preferences.
The future of stable matching looks promising, with potential advancements in both theoretical understanding and practical applications. As technology advances and the need for efficient and fair matching systems grows, the Stable Matching Problem will continue to play a crucial role in optimizing various processes across industries.
Conclusion

The Stable Matching Problem is a powerful mathematical tool with a wide range of applications. From its origins in game theory to its modern-day uses in college admissions and organ donation matching, the problem and its algorithms have proven their worth. While challenges remain, ongoing research and advancements promise to make stable matching even more efficient, fair, and adaptable to real-world complexities.
How is the Stable Matching Problem different from other matching algorithms?
+
The Stable Matching Problem is unique in that it guarantees a stable matching, ensuring that no pair of individuals would rather be matched with each other. Other matching algorithms may optimize for different criteria, such as maximizing the number of matches or minimizing the distance between matched pairs, but they do not guarantee stability.
Can the Stable Matching Problem be applied to scenarios with an unequal number of participants?
+
Yes, the Stable Matching Problem can be adapted to scenarios with an unequal number of participants. In such cases, some individuals may remain unmatched, but the matching is still stable for those who are paired.
What are some limitations of the Stable Matching Problem in real-world applications?
+
One limitation is the assumption of known and static preferences. In real-world scenarios, preferences may change over time, and there may be hidden or uncertain preferences that are not easily expressed. Additionally, the problem does not consider individual fairness, which can lead to dissatisfaction for some participants.



