Polar Moment Of Inertia Of A Square
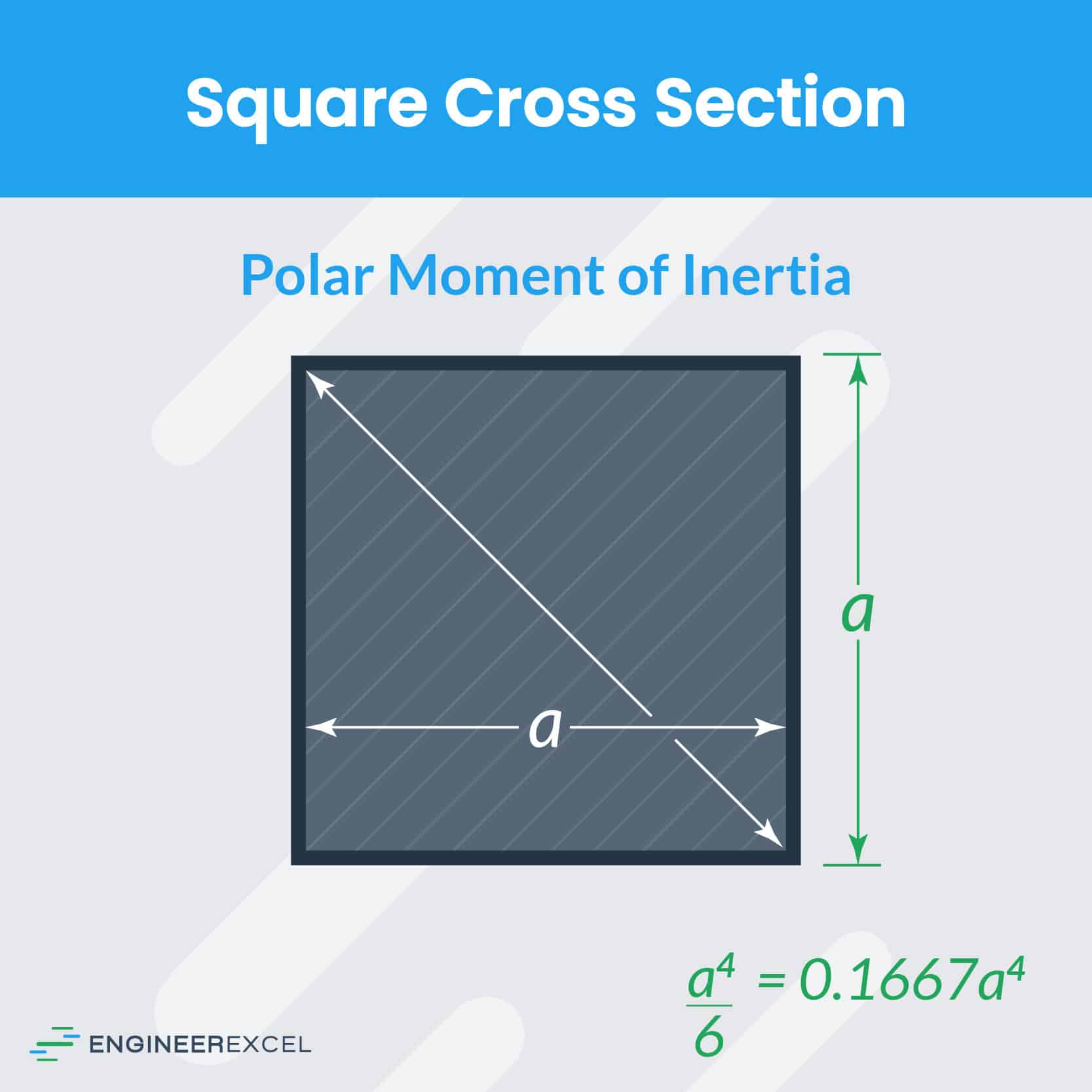
Understanding the polar moment of inertia is crucial in various engineering applications, particularly when dealing with structural analysis and designing objects that experience rotational motion. This concept plays a pivotal role in determining how objects resist twisting or torsion, a fundamental consideration in fields like mechanical engineering, civil engineering, and materials science. In this comprehensive guide, we will delve into the polar moment of inertia of a square, a geometric shape with unique properties that make it an intriguing subject of study.
The Significance of Polar Moment of Inertia
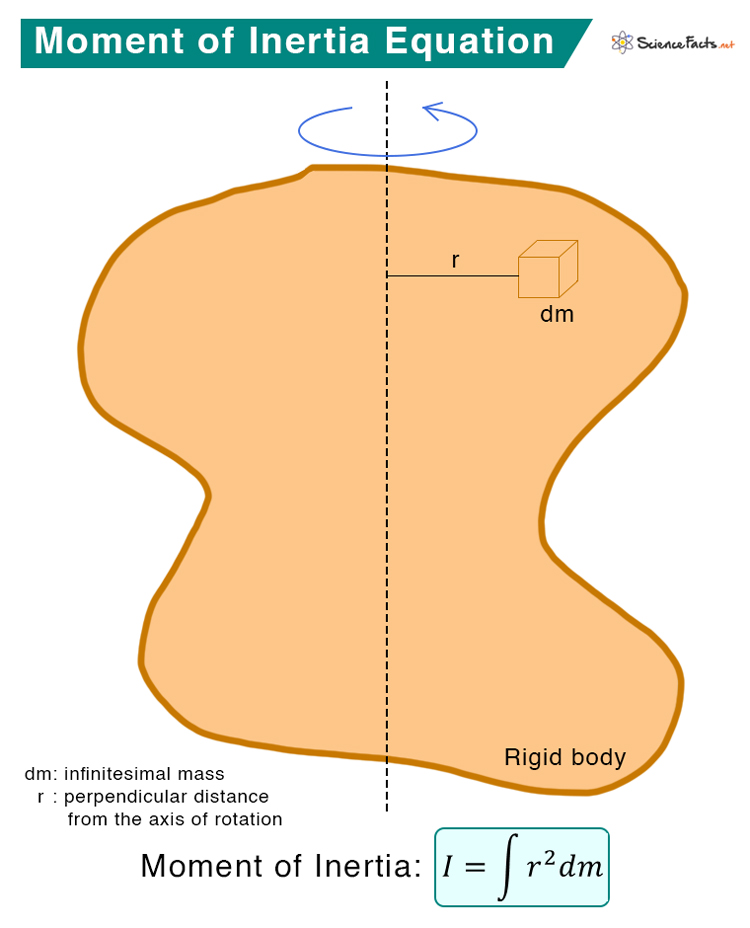
The polar moment of inertia, often denoted as J, is a measure of an object’s ability to resist torsion or twisting. It is a critical parameter in the study of mechanics, especially in the analysis of structures like beams, shafts, and columns. Engineers and designers use this value to ensure the structural integrity and safety of their creations, as excessive torsion can lead to catastrophic failures.
In simple terms, a higher polar moment of inertia indicates that an object can withstand greater twisting forces without deforming or failing. This property is especially important in the design of bridges, aircraft components, and even everyday objects like bicycle wheels, where the ability to resist torsion is essential for functionality and safety.
Mathematical Expression of Polar Moment of Inertia for a Square

The polar moment of inertia for a square can be calculated using the following formula:
\[ \begin{equation*} J = \frac{bh^3}{3} \end{equation*} \]
where b is the length of one side of the square and h is the height from the centroid to the edge of the square.
This formula is derived from the principle that the polar moment of inertia for a square is directly proportional to the square of its dimensions. The 1/3 term is a constant that accounts for the distribution of mass in the square.
For example, let's consider a square with a side length of 5 meters. The height from the centroid to the edge, h, would be 2.5 meters (half the diagonal length). Plugging these values into the formula, we get:
\[ \begin{align*} J &= \frac{5 \text{ m} \times (2.5 \text{ m})^3}{3} \\ &= \frac{5 \text{ m} \times 15.625 \text{ m}^3}{3} \\ &\approx 128.47 \text{ m}^4 \end{align*} \]
Therefore, the polar moment of inertia for this square is approximately 128.47 m4.
Applications and Real-World Examples
The concept of polar moment of inertia finds extensive use in various real-world scenarios. Here are a few examples:
Bridge Design
When designing bridges, engineers must consider the torsion that can occur due to wind loads or vehicle traffic. A bridge with a high polar moment of inertia will be more resistant to twisting and will maintain its structural integrity under these loads.
Rotor Design in Aircraft
In aircraft engineering, the rotor blades of helicopters and certain aircraft types experience significant torsion during operation. The polar moment of inertia of these blades is a critical factor in ensuring they can withstand the torsional stresses without failing.
Structural Design of Buildings
Buildings, especially tall structures, can experience twisting due to wind loads. A building’s structural elements, like beams and columns, are designed with appropriate polar moments of inertia to resist these twisting forces.
Square-Shaped Shafts in Machinery
In mechanical systems, square-shaped shafts are used in certain applications. The polar moment of inertia of these shafts is a key consideration in the design process to ensure they can transmit power efficiently without excessive deformation.
Comparative Analysis: Polar Moment of Inertia of Different Shapes
The polar moment of inertia varies significantly depending on the shape of the object. Here’s a comparison of the polar moment of inertia for a few common shapes:
| Shape | Polar Moment of Inertia Formula |
|---|---|
| Square | J = (b^2 * h^2) / 3 |
| Circle | J = (π * r^4) / 2 |
| Rectangle | J = (b^2 * h^2) / 12 |
| Triangle | J = (b^2 * h^2) / 36 |
From this table, we can see that the polar moment of inertia for a square is relatively higher compared to other shapes, especially when the sides of the square are longer. This makes squares and rectangular shapes more resistant to torsion, which is why they are often preferred in structural designs where torsional stiffness is crucial.
Future Implications and Research
The study of polar moment of inertia is an ongoing area of research, particularly in the field of computational mechanics and material science. With advancements in technology and simulation software, engineers can now model and analyze complex shapes and structures with greater accuracy. This allows for more efficient designs and a better understanding of how objects behave under various loading conditions.
Furthermore, the concept of polar moment of inertia is not limited to solid objects. It is also applied in fluid dynamics and electromagnetism, where the distribution of mass or charge plays a crucial role in the behavior of the system. Researchers are exploring new methods and materials to optimize the polar moment of inertia in various applications, leading to innovations in structural design and material science.
In conclusion, the polar moment of inertia is a vital parameter in the design and analysis of structures and objects. By understanding this concept and its application, engineers and scientists can create safer, more efficient, and more innovative solutions in various industries. The future of structural engineering and material science looks promising, with continuous advancements and discoveries in this field.
What is the significance of the polar moment of inertia in engineering design?
+The polar moment of inertia is crucial in engineering design as it determines an object’s resistance to torsion or twisting. In structures like bridges, aircraft components, and machinery, a high polar moment of inertia ensures that the object can withstand these forces without deforming or failing, thus maintaining structural integrity and safety.
How does the polar moment of inertia vary for different shapes?
+The polar moment of inertia varies depending on the shape and dimensions of the object. For example, a square has a higher polar moment of inertia compared to a triangle or a circle of the same dimensions. This is due to the distribution of mass within the shape, which affects its resistance to torsion.
Why is the polar moment of inertia important in fluid dynamics and electromagnetism?
+In fluid dynamics, the polar moment of inertia is used to analyze the behavior of fluids under rotational motion. In electromagnetism, it is applied to understand the distribution of charge or current in a system, especially in the design of electrical machines and devices.



