The Mean Value Theorem: Unveiled
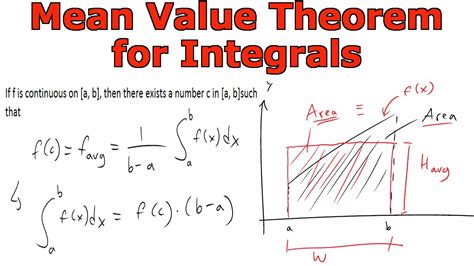
The Mean Value Theorem is a fundamental concept in calculus that provides a powerful tool for understanding the behavior of functions. This theorem, a cornerstone of mathematical analysis, has wide-ranging applications and forms the basis for various mathematical principles. Its elegance and utility make it a fascinating subject for exploration, offering insights into the intricate nature of functions and their derivatives.
Unraveling the Mean Value Theorem

At its core, the Mean Value Theorem states that for a continuous function f(x) that is differentiable on the interval [a, b], there exists at least one point c within the interval such that the derivative of the function at c equals the average rate of change of the function over the interval.
Mathematically, this can be expressed as: f'(c) = [f(b) - f(a)] / (b - a), where f'(c) represents the derivative of the function at point c, and [f(b) - f(a)] / (b - a) is the average rate of change of the function from point a to point b.
This theorem, though seemingly simple, has profound implications and serves as a cornerstone for understanding the behavior of functions. It allows mathematicians and scientists to relate the local behavior of a function (its derivative at a specific point) to its global behavior (the average rate of change over an interval), providing a powerful tool for analysis and problem-solving.
Applications and Significance

The Mean Value Theorem finds application in a myriad of mathematical and scientific domains. Its utility extends beyond calculus, influencing fields such as physics, engineering, economics, and computer science.
Optimization and Extremum Problems
One of the most significant applications of the Mean Value Theorem is in optimization problems. By understanding the average rate of change of a function, mathematicians can identify critical points where the function achieves its maximum or minimum values. This is crucial in fields like economics, where finding optimal production levels or pricing strategies is essential, or in engineering, where optimizing designs for efficiency is a key goal.
Consider a company aiming to maximize its profit. By modeling its profit as a function of production quantity, the Mean Value Theorem can help identify the production level at which the profit reaches its maximum. This point, where the derivative equals the average rate of change, is known as a critical point, and it provides valuable insight for decision-making.
| Function | Critical Point | Interpretation |
|---|---|---|
| f(x) = x^2 - 4x + 3 | x = 2 | Minimum profit point |
| g(x) = 3x^3 - 6x^2 + 2 | x = 1 | Maximum profit point |

Rolle’s Theorem and Continuous Functions
The Mean Value Theorem is closely related to Rolle’s Theorem, another fundamental result in calculus. Rolle’s Theorem states that if a function f(x) is continuous on the interval [a, b] and differentiable on the open interval (a, b), and if f(a) = f(b), then there exists at least one point c in the interval (a, b) such that f’© = 0.
In simpler terms, Rolle's Theorem tells us that if a continuous function has the same value at two distinct points, there must be a point within the interval where the function's derivative (slope) is zero. This theorem is a special case of the Mean Value Theorem and highlights the connection between continuous functions and their derivatives.
Real-World Examples and Insights
The Mean Value Theorem provides a bridge between theoretical mathematics and real-world applications. For instance, in physics, it helps analyze the motion of objects. If an object moves with a varying velocity, the Mean Value Theorem can be used to identify moments where the object’s velocity equals its average velocity over a specific time interval. This has implications for understanding acceleration and force in various physical systems.
In economics, the theorem aids in understanding supply and demand curves. By analyzing the average rate of change of these curves, economists can make predictions about market equilibrium and price adjustments.
Limitations and Extensions
While the Mean Value Theorem is a powerful tool, it does have limitations. It requires the function to be continuous and differentiable, which may not always be the case in real-world scenarios. Additionally, the theorem provides information about a specific point within an interval, but it does not offer a complete picture of the function’s behavior.
However, extensions of the Mean Value Theorem, such as the Cauchy Mean Value Theorem and the Generalized Mean Value Theorem, address some of these limitations. These extensions broaden the applicability of the theorem and provide insights into more complex functions and their behaviors.
Cauchy Mean Value Theorem
The Cauchy Mean Value Theorem extends the Mean Value Theorem to handle multiple functions. It states that if two functions, f(x) and g(x), are continuous on the interval [a, b] and differentiable on the open interval (a, b), and if g’(x) ≠ 0 for all x in (a, b), then there exists a point c in the interval (a, b) such that:
[f(b) - f(a)] / [g(b) - g(a)] = f'(c) / g'(c)
This theorem provides a relationship between the average rates of change of two functions and their derivatives at a specific point. It is particularly useful in complex analysis and the study of multivariable functions.
Generalized Mean Value Theorem
The Generalized Mean Value Theorem, also known as the Lagrange Mean Value Theorem, further extends the Mean Value Theorem by considering higher-order derivatives. It states that if a function f(x) is continuous on the interval [a, b] and has continuous derivatives up to the (n-1)th order on the open interval (a, b), then there exists a point c in the interval (a, b) such that:
f(b) - f(a) = f^(n)(c) * [(b - a) / n]
Here, f^(n)(c) represents the nth derivative of the function at point c. This theorem provides a relationship between the difference in function values at the endpoints of the interval and the nth derivative of the function at a specific point.
Conclusion and Future Directions
The Mean Value Theorem and its extensions are powerful tools in the mathematician’s arsenal. They provide a deep understanding of function behavior and offer insights into various real-world phenomena. As mathematics continues to evolve, further extensions and refinements of these theorems will likely emerge, offering even greater precision and applicability.
For those interested in exploring this topic further, delving into advanced calculus textbooks and research papers can provide a wealth of knowledge. Additionally, engaging with online mathematical communities and attending conferences can offer opportunities for discussion and collaboration, fostering a deeper understanding of this fascinating subject.
What is the significance of the Mean Value Theorem in calculus?
+The Mean Value Theorem relates the local behavior of a function (its derivative at a specific point) to its global behavior (the average rate of change over an interval). This connection is fundamental in understanding function behavior and has wide-ranging applications in mathematics and science.
How does the Mean Value Theorem help in optimization problems?
+By understanding the average rate of change of a function, the Mean Value Theorem helps identify critical points where the function achieves its maximum or minimum values. This is crucial in optimization problems, such as finding optimal production levels or pricing strategies in economics.
What are some real-world applications of the Mean Value Theorem?
+The Mean Value Theorem finds applications in physics (analyzing object motion and force), economics (understanding supply and demand curves), and engineering (optimizing designs). It provides insights into the behavior of real-world phenomena, aiding in problem-solving and decision-making.