Understanding the Robinson Map Projection
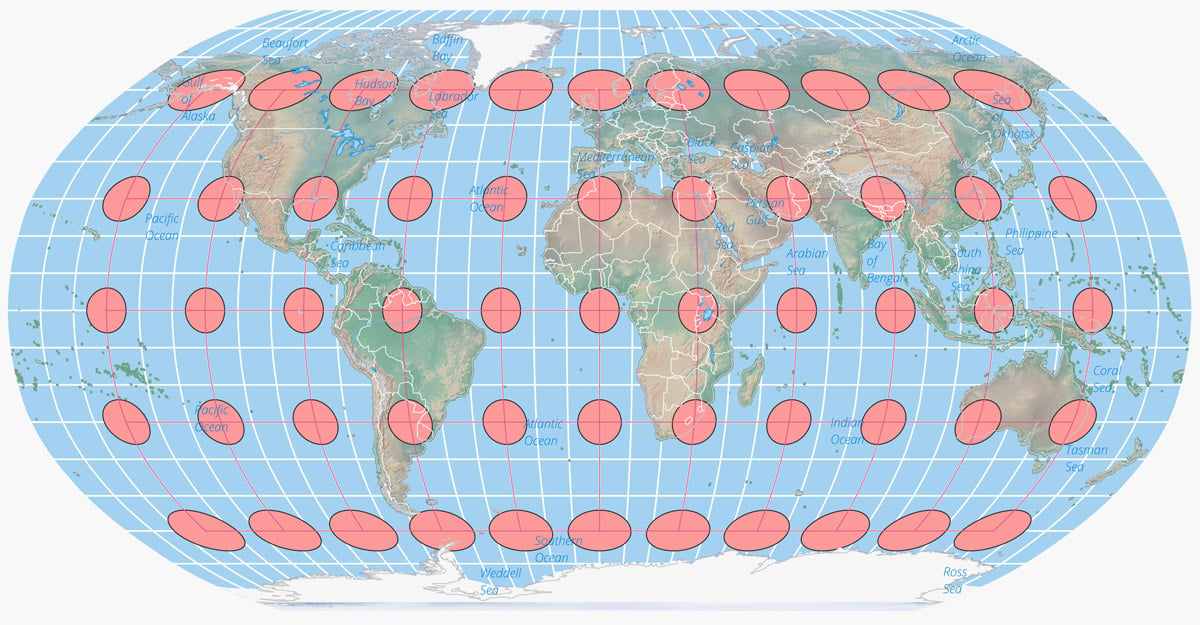
In the vast world of cartography, the art and science of mapmaking, various map projections have been developed to represent the spherical Earth on a flat surface. Among these projections, the Robinson Map Projection stands out as a unique and widely recognized tool, offering a distinct perspective on our planet.
The Robinson Map Projection: A Brief Overview

The Robinson Map Projection, or simply the Robinson projection, is a distinctive type of map projection developed by Arthur H. Robinson, an American cartographer, in 1963. Robinson aimed to create a projection that would provide a visually appealing and easily understandable representation of the Earth’s surface, suitable for general reference maps.
This projection is a compromise between several key aspects of map projection, including area, direction, distance, and shape. It strikes a balance, aiming to minimize distortion across the globe while maintaining a visually pleasing and simple appearance. This projection's unique characteristics have made it a popular choice for world maps, especially in educational settings and atlases.
The Development and Impact of the Robinson Projection

Arthur H. Robinson’s motivation for developing this projection was to address the shortcomings of existing map projections. Traditional projections like the Mercator, popular for its ability to preserve direction and angles, often distorted the size of landmasses, particularly near the poles. On the other hand, conformal projections like the Lambert conformal conic or the Albers equal-area conic, while accurate in specific regions, were not suitable for representing the entire globe.
Robinson's innovation lay in his use of mathematical algorithms to calculate the positions of points on the map, ensuring a balanced representation of both polar regions and the equator. This approach, coupled with a unique graticule design, resulted in a map that offers a more accurate portrayal of the Earth's size and shape compared to previous projections.
The Robinson projection's impact was immediate and significant. It quickly gained popularity among cartographers and map users, becoming a standard projection for many world maps and atlases. Its visual appeal and accuracy made it a preferred choice for various applications, from educational resources to decorative wall maps.
Key Characteristics of the Robinson Map Projection
The Robinson projection is characterized by its distinctive appearance, with continents and oceans appearing as a series of gently curved lines. This projection is pseudocylindrical, meaning it resembles a cylinder that has been slightly flattened at the poles. It is neither equal-area nor conformal, but it approximates both properties, reducing distortion to a minimum.
One of the notable features of the Robinson projection is its preservation of shape and size. While it does not perfectly maintain the relative sizes of continents, it does so to a greater extent than many other projections. This characteristic makes it particularly useful for maps where the accurate portrayal of landmasses is important, such as in political or physical geography.
| Property | Description |
|---|---|
| Area | Preserves area to some extent, but not perfectly. |
| Shape | Maintains the shape of continents and oceans reasonably well. |
| Direction | Preserves direction, but not perfectly. |
| Distance | Distances are not accurate on this projection. |

Technical Specifications and Formulas
The Robinson projection is defined by a set of mathematical formulas that describe the transformation of points from a spherical Earth model to a flat map. These formulas ensure the projection’s distinctive appearance and its balanced representation of various map properties.
The projection is based on the following mathematical equation, which calculates the x and y coordinates of a point on the map:
$$ \begin{equation*} x = \frac{3\lambda}{2}\sqrt{2} \cos(\varphi) \left( \frac{1}{3} - \frac{1}{3}\cos(2\varphi) \right) + \sqrt{2}\sin(\varphi) \left( \frac{3}{2} - \frac{3}{2}\cos(2\varphi) \right) \end{equation*} $$
$$ \begin{equation*} y = \frac{3\lambda}{2}\sqrt{2} \sin(\varphi) \left( \frac{1}{3} - \frac{1}{3}\cos(2\varphi) \right) + \sqrt{2}\cos(\varphi) \left( \frac{3}{2} - \frac{3}{2}\cos(2\varphi) \right) \end{equation*} $$
where $\lambda$ is the longitude and $\varphi$ is the latitude of the point on the Earth's surface.
The above formulas use the following parameters and transformations:
- Longitude ($\lambda$): This is the angle, measured in degrees, representing the horizontal position of a point on the Earth's surface.
- Latitude ($\varphi$): This is the angle, measured in degrees, representing the vertical position of a point on the Earth's surface.
- Cosine ($\cos$): This is a trigonometric function that calculates the cosine of an angle.
- Sine ($\sin$): This is a trigonometric function that calculates the sine of an angle.
The Robinson projection's mathematical formulation ensures that the map's distortion is minimized, providing a visually appealing and relatively accurate representation of the Earth's surface.
Performance and Applications
The Robinson projection’s performance is excellent for its intended purpose – general-purpose world maps. It provides a balanced representation of various geographic features, making it suitable for a wide range of applications. Some of its key strengths include:
- Visual Appeal: The projection's distinctive curved lines and balanced appearance make it aesthetically pleasing, which is an important consideration for maps used in educational settings or for decorative purposes.
- Accurate Shape and Size: While it does not perfectly preserve area or shape, the Robinson projection maintains these properties to a greater extent than many other projections. This makes it suitable for maps where an accurate representation of landmasses is crucial.
- Versatility: Due to its balanced nature, the Robinson projection can be used for a variety of map types, including political, physical, and thematic maps. Its versatility makes it a go-to choice for many cartographers and map users.
Specific Applications
The Robinson projection has found use in a variety of specific applications, including:
- Educational Atlases: Its visual appeal and accuracy make it a popular choice for atlases used in schools and educational institutions. These maps provide a clear and understandable representation of the world, aiding in the teaching of geography and global awareness.
- General Reference Maps: Whether for wall-mounted maps in offices or online maps for quick reference, the Robinson projection's balance and simplicity make it an ideal choice. It provides a quick, easily understandable overview of the world's geography.
- Thematic Maps: The Robinson projection can be used for thematic maps, such as those depicting climate zones, population density, or natural resources. Its ability to maintain the shape and relative size of landmasses makes it suitable for these types of maps.
Comparative Analysis: Robinson vs. Other Projections

When compared to other popular map projections, the Robinson projection offers a unique set of advantages and trade-offs. Here’s a comparative analysis of the Robinson projection against some of the most common map projections:
Robinson vs. Mercator
The Mercator projection, developed in the 16th century, is one of the most well-known map projections. It is conformal, meaning it preserves angles and shapes, making it ideal for navigation. However, it greatly distorts the size of landmasses, particularly near the poles.
In contrast, the Robinson projection aims to balance various map properties, including area, shape, and direction. While it does not perfectly preserve any of these properties, it reduces distortion across the globe. This makes the Robinson projection a better choice for general-purpose world maps, where an accurate portrayal of landmasses is important.
Robinson vs. Equal-Area Projections
Equal-area projections, such as the Albers equal-area conic or the Gall-Peters projection, aim to accurately represent the relative sizes of landmasses. These projections are ideal for maps where the accurate portrayal of area is crucial, such as in demographic or resource distribution maps.
The Robinson projection, while not an equal-area projection, does maintain the relative sizes of landmasses to a greater extent than many other projections. This balance makes it a more versatile choice, suitable for a wider range of map types, including those where area accuracy is important but not the primary focus.
Robinson vs. Conformal Projections
Conformal projections, such as the Lambert conformal conic, preserve angles and shapes, making them ideal for navigation and weather maps. However, they often distort area and distance.
The Robinson projection, while not conformal, does maintain the shape of continents and oceans to a reasonable degree. This balance between shape preservation and other map properties makes it a more visually appealing and understandable choice for general-purpose world maps.
Future Implications and Alternatives
Despite its popularity and unique advantages, the Robinson projection is not without its limitations. Its trade-off between various map properties means that it may not be the best choice for all map applications. As such, cartographers and map users continue to explore and develop new projections to meet specific needs.
One notable alternative is the Winkel tripel projection, developed in the 1920s. Similar to the Robinson projection, the Winkel tripel aims to balance various map properties. It is neither conformal nor equal-area, but it minimizes distortion, making it a popular choice for world maps. The Winkel tripel has gained prominence in recent years, particularly in educational settings.
Another alternative is the Gall-Peters projection, which is an equal-area projection. This projection aims to accurately represent the relative sizes of landmasses, providing a more realistic portrayal of the world's geography. While it has gained popularity for its social and political implications, it has also been criticized for its distortion of shapes and angles.
As the field of cartography continues to evolve, new projections will undoubtedly be developed, offering even more accurate and visually appealing representations of our world. The Robinson projection, while a significant contribution to the field, is just one of many tools available to cartographers, each with its own unique strengths and limitations.
What is the Robinson projection commonly used for?
+The Robinson projection is commonly used for general-purpose world maps, especially in educational settings and atlases. Its visual appeal and balanced representation of various geographic features make it a versatile and popular choice.
How does the Robinson projection compare to the Mercator projection?
+While the Mercator projection is conformal and ideal for navigation, it greatly distorts the size of landmasses, particularly near the poles. The Robinson projection aims to balance various map properties, reducing distortion across the globe. This makes the Robinson projection a better choice for general-purpose world maps where an accurate portrayal of landmasses is important.
What are some alternatives to the Robinson projection?
+Some alternatives to the Robinson projection include the Winkel tripel projection, which also aims to balance various map properties, and the Gall-Peters projection, which is an equal-area projection. Each projection has its own unique strengths and limitations, and the choice depends on the specific needs and purpose of the map.



