5 Quick Steps: Gram-Schmidt Orthogonalization
In the realm of linear algebra and matrix operations, the Gram-Schmidt orthogonalization process stands as a powerful technique with diverse applications. This method, often referred to as the Gram-Schmidt process, transforms a set of linearly independent vectors into an orthogonal set, offering a unique perspective on vector spaces and their transformations.
The Gram-Schmidt Orthogonalization Process: A Concise Overview

At its core, the Gram-Schmidt process is a systematic approach to creating an orthogonal basis for a given subspace. Orthogonalization, in this context, refers to the process of making vectors perpendicular to each other, which is a crucial step in many mathematical and computational problems. This process finds extensive use in various fields, from quantum mechanics and signal processing to numerical analysis and computer graphics.
A Step-by-Step Guide to Gram-Schmidt Orthogonalization
Here’s a simplified breakdown of the Gram-Schmidt process, step by step:
- Initialize: Start with a set of linearly independent vectors v1, v2, …, vn that span a given subspace. These vectors will be transformed into an orthogonal set.
- Calculate the First Orthogonal Vector: For the first vector, calculate u1 = v1. This step is straightforward as the first vector is already considered orthogonal.
- Iterate for the Remaining Vectors: For each subsequent vector vi (where i ranges from 2 to n), calculate the orthogonal projection onto the subspace spanned by the previous orthogonal vectors. This projection is given by ui = vi - (u1 · vi)u1 - (u2 · vi)u2 - … - (ui-1 · vi)ui-1, where · represents the dot product.
- Normalize the Orthogonal Vectors: After obtaining the orthogonal vectors ui, normalize them to ensure they have unit length. This is done by dividing each vector by its magnitude: ui = ui / ||ui||, where ||ui|| is the Euclidean norm of ui.
- Repeat until Convergence: Continue this process until all vectors in the original set have been transformed into their respective orthogonal counterparts. This typically results in an orthogonal set u1, u2, …, un that spans the same subspace as the original vectors.
It's important to note that the Gram-Schmidt process is an iterative algorithm and its convergence depends on the linear independence of the input vectors. If the input vectors are linearly dependent, the process may fail to produce an orthogonal set.
The Practical Implications and Applications
The Gram-Schmidt process has wide-ranging applications across various disciplines. In quantum mechanics, it is used to construct orthogonal bases for Hilbert spaces, aiding in the solution of quantum mechanical problems. In signal processing, it finds use in the design of filters and the analysis of signals. Additionally, in computer graphics, it is employed for tasks such as 3D rotation and reflection.
| Application | Industry |
|---|---|
| Quantum Mechanics | Physics, Engineering |
| Signal Processing | Telecommunications, Audio/Video Processing |
| Computer Graphics | Gaming, Film, Animation |

Furthermore, the Gram-Schmidt process serves as a fundamental tool in numerical linear algebra, particularly in the context of numerical analysis. It is often utilized in algorithms such as the QR decomposition and the singular value decomposition (SVD), which are essential for solving linear systems and analyzing data.
The Mathematical Elegance of Orthogonalization
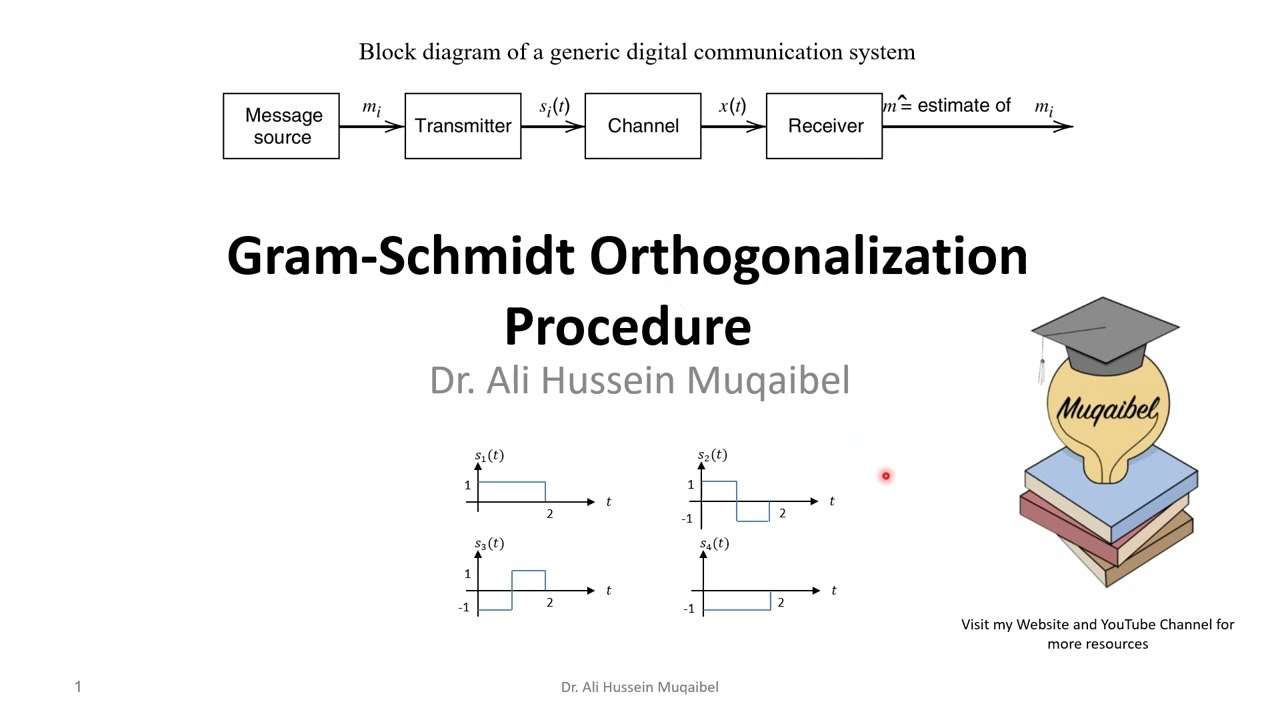
The Gram-Schmidt process, despite its simplicity, is a testament to the beauty and utility of mathematical techniques. By transforming a set of vectors into an orthogonal basis, it provides a more structured and organized representation of the underlying space. This transformation is particularly useful in high-dimensional spaces, where the simplicity and predictability of orthogonal vectors can greatly simplify computations and analysis.
The process also serves as a bridge between different mathematical concepts. For instance, it connects linear algebra with the theory of inner product spaces, offering a deeper understanding of vector spaces and their properties. Additionally, the Gram-Schmidt process has inspired further research and developments in the field, leading to more advanced and efficient algorithms for orthogonalization and other related tasks.
A Historical Perspective
The Gram-Schmidt process is named after two mathematicians, Jørgen Pedersen Gram and Erhard Schmidt, who independently developed the method in the late 19th and early 20th centuries. Gram, a Danish mathematician, initially proposed the method in 1883 as a way to solve systems of linear equations. Schmidt, a German mathematician, later expanded upon Gram’s work, developing a more general version of the process in 1907.
Since its inception, the Gram-Schmidt process has become a cornerstone of linear algebra and its applications. Its simplicity, effectiveness, and versatility have made it a go-to technique for many mathematicians, scientists, and engineers. Today, it continues to be a fundamental tool in various fields, from the theoretical underpinnings of mathematics to the practical applications of engineering and computer science.
Future Prospects and Innovations
As computational power and mathematical understanding continue to advance, the Gram-Schmidt process and its variants are likely to remain a central component of many mathematical and computational methods. New developments, such as fast algorithms and parallel implementations, are already being explored to further enhance the efficiency and applicability of orthogonalization techniques.
Furthermore, the Gram-Schmidt process and related methods are being extended to more complex and diverse spaces, such as infinite-dimensional Hilbert spaces and non-Euclidean geometries. These extensions are opening up new avenues of research and applications, pushing the boundaries of what is possible with orthogonalization techniques.
In conclusion, the Gram-Schmidt orthogonalization process is a powerful and versatile tool with a wide range of applications. Its ability to transform a set of vectors into an orthogonal basis provides a structured and organized framework for understanding and manipulating vector spaces. As we continue to explore the depths of linear algebra and its applications, the Gram-Schmidt process and its variants will undoubtedly play a crucial role in our mathematical and computational endeavors.
What is the main purpose of the Gram-Schmidt process?
+
The primary purpose of the Gram-Schmidt process is to transform a set of linearly independent vectors into an orthogonal set, which is a crucial step in various mathematical and computational problems.
How is the Gram-Schmidt process applied in real-world scenarios?
+
The Gram-Schmidt process finds extensive use in fields such as quantum mechanics, signal processing, computer graphics, and numerical analysis. For instance, it is used to construct orthogonal bases for Hilbert spaces in quantum mechanics, design filters in signal processing, and perform 3D rotations in computer graphics.
What are the key advantages of using the Gram-Schmidt process?
+
The Gram-Schmidt process offers a systematic and efficient approach to orthogonalization, providing a structured representation of vector spaces. This simplifies computations and analysis, particularly in high-dimensional spaces, and has applications across various disciplines.



